決定木

決定木の概要

　決定木とは、特定の特徴がよく現れるようなデータのかたまりを見つけ、その分類ルールを生成する機械学習の手法です。具体的には、目的変数と説明変数を設定し、目的変数の特徴が固まって存在するようなデータグループを見つけていくのですが、複数の説明変数を使った条件でデータを分割していくことで、そのデータ領域内における目的変数の特徴の濃度を高めていきます。言い換えますと、目的変数の特徴がなるべく偏るようなデータ領域となるように、つまりその領域内のデータのばらつきが小さくなるように、説明変数の条件を組み合わせて分割していきます。そうして得られた説明変数の条件で構成されるデータの分岐ルール（If-Thenの条件ルール）をツリー構造で生成する手法が決定木です。

分類木と回帰木

　決定木には分類木と回帰木という2つのタイプがあります。分類木では目的変数に離散値となる質的変数を取り、回帰木では目的変数に連続値となる量的変数を取ります。なお、説明変数には質的変数も量的変数もどちらも取ることができます。分類木では目的変数（質的変数）の各カテゴリの該当割合に違いが出るようにデータを分割していきます。特に「YesかNo」「該当ありか該当なし」「1か0」といった2水準のフラグ変数を目的変数に取る例が多いです。つまり、「1：該当あり」の割合が大きく偏るようなデータ領域を見つけていきます。一方で回帰木では、目的変数（量的変数）の値が偏るように、つまり値のばらつきが小さくなるようなデータ領域を見つけていき、各データ領域内の値の平均値を期待値として評価します。決定木の分類木と回帰木それぞれの用途の関係は、回帰分析で言うロジスティック回帰分析と重回帰分析の関係に近いと言えます。回帰分析は説明変数の線形結合に基づく回帰式で目的変数の特徴を説明しますが、決定木では説明変数の条件に基づくデータの分割で目的変数の特徴を説明していきます。

　より具体的に下図のイメージ図を使って分類木と回帰木について説明します。このイメージ図では、ある店舗で使えるクーポン付きDM（ダイレクトメール）を顧客に送付したときに、そのうち何割の顧客がそのDMに反応して来店したのか、そして来店した顧客はその店舗でいくら購入したのか、ということについてその特徴と要因を決定木で分析した例です。

　左の分類木では、目的変数は「クーポン付きDMの反応有無（1：反応あり、0：反応なし）」としており、図の中の１つの〇が1件のデータを表していて、〇の中に1か0の値が入っています。この図は変数空間上のデータの配置を表していて、ここでは40個の〇があるので40件のデータということです。説明変数には「送付したクーポンの割引率」や「送付した顧客の年齢」などがあったとします。例えば、クーポンの割引率が20%というラインでデータを分割すると、割引20%以上では反応する顧客が多いデータ領域（右側）が切り出されます。割引20%未満のデータ領域（左側）については、さらに年齢が32歳というラインでデータを分割すると、32歳以上では反応する顧客がやや多いデータ領域（左上）が、32歳未満では反応する顧客が少ないデータ領域（左下）が切り出されます。こうして切り出されたそれぞれのデータ領域における反応顧客の割合（反応率）には偏りが生まれます。このデータの分岐ルールをツリー構造で可視化したものが決定木のアウトプットになります。

　右の回帰木では、先ほどの分類木でDMに反応した顧客28件について、その顧客が店舗に来店したときにいくら購入したのかということを対象としたもので、目的変数は「来店顧客の購入金額」としています。先ほどと同様に変数空間上のデータの配置を示す図では、1つの〇が1件のデータを表していますが、回帰木では目的変数は量的変数になるため、〇の中には購入金額（単位：千円）という連続値が入っており、〇の大きさはその値の大きさに対応しています。今回は説明変数に「顧客の昨年の来店頻度」や「顧客の年齢」などがあったとします。例えば、昨年の来店頻度が16回というラインでデータを分割すると、16回以上では購入金額が多いデータ領域（右側）が切り出されます。来店頻度16回未満のデータ領域（左側）については、さらに年齢が48歳というラインでデータを分割すると、48歳以上では購入金額がやや多いデータ領域（左上）が、48歳未満では購入金額が少ないデータ領域（左下）が切り出されます。こうして切り出されたそれぞれのデータ領域における購入金額はばらつきが小さく偏っており、それぞれの平均購入金額にも大きな差が現れます。決定木では、こうしたデータの分岐ルールをツリー構造で可視化します。

　決定木のツリー図では、それぞれのデータグループを「ノード」、特に最初のデータ全体を指すノードを「ルートノード」、分岐が止まった一番末端にあるノードを「リーフノード」とか「ターミナルノード」といいます。またあるノードに対して、分岐前のノードを親ノード、分岐後のノードを子ノード、ツリーの枝となる分岐のラインを「エッジ」といいます。

決定木のメリット

　決定木はデータ分類のクラスタリングや予測・判別のモデリング、要因関係の可視化など、様々な分析目的で適用できる万能ともいえる分析手法で、以下に挙げるような多くのメリットがあります。

①教師ありのクラスタリングを実行できる
　データクラスタリングは通常教師なし学習という計算を実行し、データ全体の特徴からそのデータをいくつかのクラスタに分類するもので、何か分類のターゲットを定めているわけではありません。一方、決定木ではある目的変数に対して特徴的な分類を見つけることができます。例えば売上の規模に応じたデータ分類を売上以外の変数を使って実行したり、リピート率の高さに応じた顧客分類をリピート率以外の変数を使って実行するということができます。つまりビジネスアクションに直結するようなターゲット指標（目的変数）に対して最も効果的なデータ分類の仕方を他の説明変数を使って導くことができます。

②ターゲットに対して最も効果的な切り口を発見できる
　目的変数に定めたターゲットに対して、もっともその特徴が現れるような細かいルール、複合要因、セグメントを見つけることができます。つまりデータの中から最も注目したい領域の切り口を見つけることができます。特にある条件とある条件が揃うことで効果が発揮されるという場合でもそうした複合条件を抽出できます。例えば、リピート率が高い顧客属性は女性であることが分かっていても、単純に女性というだけでなく、女性のうち特にリピート率が高いのは20代30代であり、さらにその中でも未婚者のリピート率が高いということや、逆に女性の50代60代はリピート率が低いということ、しかしその中でも水曜日に発行されるクーポンを受け取るとリピート率が上昇するということなど、効果を高めるより詳細な条件を導出することができます。これにより、どのような顧客をターゲットにすべきか、どのような施策が効果を発揮するのかという戦略を講じることができます。
　データ分析ではよく層別の分析という属性の条件別に分けた分析をします。例えば全体で相関係数を求めて相関が低い場合でも、男性と女性に分けて相関係数をそれぞれ求めると高い相関が得られるというように、全体では特徴が見えなかった結果も、属性別に分析することで意味のある結果が得られることが多くあります。たいていそのような層別の分析では、分析者の仮説に基づいて分析の切り口を探していきます。ただ、人間が検討できる層別はせいぜい１階層程度ですし、そうした切り口は人間ならではの経験や感覚のバイアスがかかったものとなりがちです。決定木ではその有力な切り口を複数階層で探すことができ、またそこには客観性もあります。これはビジネス場面ではとても有用なことが多いものと思われます。

③ターゲットに対して効果的な量的説明変数の閾値を自動で計算できる
　上記のメリットとも共通することですが、ターゲットに対して効果的な切り口を探索する場合、その切り口の対象となる変数が量的変数であれば、通常は人間の経験的な閾値を採用した切り方が検討されます。例えば商品購買に対して、年代であれば、10代、20代、30代というように10歳刻み、商品の価格であれば1,000円未満、1,000円～3,000円、3,000円～5,000円というように数千円刻み、というようにその閾値の切り方が正しいかどうかは分からないものの、何となくキリが良いという理由でこうした切り方が採用されることが多いかと思います。しかし実際は、年代は22歳以下、23歳～28歳、29歳～36歳という切り方のほうが商品購買の特徴をうまく説明できているかもしれませんし、この年代の切り方の閾値も商品の価格によって変動するかもしれません。決定木ではこうした量的変数について、ターゲット（目的変数）に対して最も効果的な切り方の閾値を自動で計算することができ、その閾値も各条件によって最適なものを見つけてくれます。これは業務にデータ分析を活用する上でかなり強力な機能といえます。例えば機械の稼働ログデータから機械の故障予測や保守点検などに決定木を活用することを考えた場合、機械のどのセンサの値がどれくらいの値を超えると故障率が上昇するか、つまりアラートを出すべきセンサの閾値はいくつかといったルールを見つけることができます。

④非線形のデータ処理のため、線形関係のない現象でも特徴を抽出できる
　例えばリピート率と年齢の関係を分析する場合、データ分析の入門とも言える回帰分析などでは、リピート率と年齢に線形関係（比例関係）があることで初めて効果があると判定されますが、決定木では年齢の中でも、25歳近辺と40歳近辺に限ってリピート率が高いといった、線形関係になくても効果が強く現れる特定の領域を見つけることができます。

⑤高次元なデータでも比較的高速に計算できる
　これは分析に使用するPCのスペックや分析ツールにも依存しますが、決定木ではとても多くの変数で構成される高次元なデータでも比較的高速に分析ができる印象があります。より効果的な分岐ルールを発見するため、元々ある説明変数に加えてその派生変数も作成し、数百数千ほどの説明変数に対して分析することもあります。

⑥外れ値の影響が少ない
　決定木では、データを分割することによって特徴を顕在化させるため、データの中に外れ値となるような異常に高い値や異常に低い値があったとしても、単にそうした外れ値を含むデータブロックとして分割されたり、外れ値のある領域だけが除外されるように分割されたりするので、外れ値の影響が少ない手法といえます。

⑦結果が視覚的に見やすい
　決定木は分析過程や抽出ルールがツリー構造に可視化されて見やすく、その結果を解釈しやすいこともメリットの一つです。例えば社内で分析の専門知識がない人に分析の結果や効果を説明するという場面においても、他の分析手法と比べて説明がしやすく、理解も得られやすいものと思われます。

　データ分析には様々な分析手法がありますが、困ったらとりあえず決定木、と言ってもよいくらい決定木は万能な手法だと思います。そのため様々な適用シーンで活躍し、例えば来店頻度の高い優良顧客を過去の購買情報や顧客属性から分類したり、コンビニの駐車台数、売り場面積、店頭間口などから好調店と不振店を分類したり、天気や気温、湿度、風の強さからゴルフ場に客がどれくらい来るのか予測したり、がんの発症確率を患者の属性や検査値、生活習慣から予測するなど、多様な適用事例が存在します。

決定木の例

　例えば、あるサプリの商品について初回お試し購入をした顧客が継続して同商品を購入したか否かに関するデータに決定木を適用した例を使って、決定木のアウトプットの理解をより深めていきたいと思います。
　今回は初回お試し購入をした全10,000人の顧客の購買データで、この商品を継続して購入しなかった人が5,000人、継続して購入した人が5,000人いたとします。この継続購入が目的変数となり、0：継続購入しない、1：継続購入するという2つのクラスを持つ質的変数となります。説明変数には、顧客情報として、性別、年齢、職業、また他商品Aを購入しているどうかという、質的変数と量的変数の両方があります。このデータ分析によってこの商品の継続購入の可能性が高い顧客層を特定し、マーケティング戦略を検討したいと考えます。
　決定木では、目的変数の特徴が色濃く出るように、つまり継続購入の0と1のデータがどちらかに偏るように分岐がされていくわけですが、それがうまく分かれるような説明変数、つまり関連性の強い説明変数から分岐がされます。まず性別という説明変数で、男性のグループと女性のグループに分割されました。男性のグループは4,000人で、そのうち継続購入しないが2,500人、継続購入するが1,500人と、継続購入しないほうに偏ったグループとなります。一方、女性のグループは6,000人で、そのうち継続購入しないが2,500人、継続購入するが3,500人と、継続購入するほうに偏ったグループとなります。
　決定木のツリー構造では、上位の階層にあるノードが必ず条件となります。男性のグループの下の分岐では、男性という条件下での分岐となります。この男性という条件下では、他商品Aを購入しているか否かという説明変数で分岐がされています。男性全体では継続購入しないほうに偏っていましたが、男性の他商品Aを購入している層では、継続購入しないが600人、継続購入するが900人と、継続購入するほうに偏ったグループに変化しています。一方、男性の他商品Aを購入していない層では、継続購入しないが1,900人、継続購入するが600人と、継続購入しないほうにより偏りますが、さらに男性でかつ他商品Aを購入していないという条件下での分岐を見ますと、年齢が41歳というラインで分岐がされ、男性かつ他商品Aを購入していないかつ41歳以上であると、継続購入しないが300人、継続購入するが400人と、サンプル数は少ないですが継続購入するほうに偏っているグループとなります。また、男性かつ他商品Aを購入していないかつ41歳未満であると、継続購入しないが1,600人、継続購入するが200人と、大きく継続購入しない方に偏ったグループになることが分かります。先ほども述べましたが、決定木では年齢といったような量的な説明変数については、目的変数に対して最も効果的な分岐の閾値を自動で計算してくれることが大きなメリットといえます。今回も41歳というラインが継続購入に最も影響を与えるということを機械が探索してくれましたが、これを人間が発見するのはなかなか難しいかと思います。
　続いて、女性のグループの下の分岐についても見てみます。女性全体で見ますと、継続購入する方が多いですが、これがまず年齢という説明変数で分岐され、28歳と36歳というラインで3つのグループに分割されています。女性の28歳未満では、継続購入しないが700人、継続購入するが600人と、逆に継続購入しない方に偏っています。一方、女性の28歳以上36歳未満は、継続購入しないが400人、継続購入するが700人と、継続購入により偏るようになりました。また女性の36歳以上では、継続購入しないが1,400人、継続購入するが2,200人と、継続購入するほうにやや偏っていますが、さらに職業という説明変数で分岐されると、女性かつ36歳以上かつ会社員の層では、継続購入しないが800人、継続購入するが1,700人と、大きく継続購入するほうに偏ることになり、女性かつ36歳以上かつ会社員でない層では、継続購入しないが600人、継続購入するが500人と、継続購入しないほうにやや偏っていることが分かります。
　この分析結果によって、初回お試しから継続購入の可能性が強い顧客層とは、男性では他商品Aを購入している方、あるいは他商品Aを購入していない方であっても41歳以上の方、女性については28歳以上で継続購入の可能性が高く、特に36歳以上では職業が会社員の方で継続購入の可能性がとても高いということが分かります。ここから例えば、こうした顧客層をターゲットに初回お試しの案内やキャンペーンを打つなどのマーケティング戦略を検討することができます。

決定木のアルゴリズム

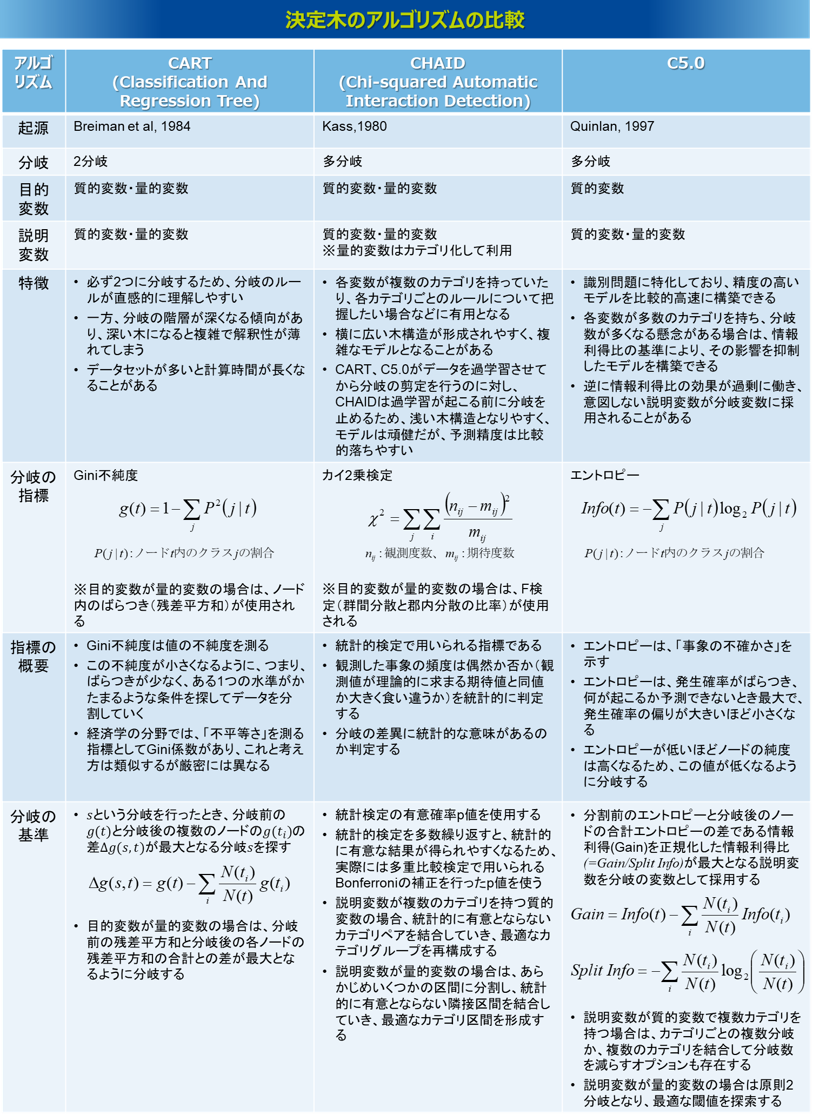
　一言で決定木と言っても様々なアルゴリズムがあり、それぞれ条件や特徴が異なります。ここではよく使用される３つのアルゴリズムCART、CHAID、C5.0を紹介します。

　CARTは、分岐される数が必ず２つとなることが特徴です。必ず２つに分岐されるため、モデルの構造がシンプルとなり、結果を理解しやすいというメリットがありますが、データセットが多いと計算時間が長くなることがあります。分岐の指標にはジニ係数を使います。ジニ係数は経済学の分野で用いられる「不平等さ」を測る指標で、0から1の値をとり、0に近いほど平等となります。決定木において、Gini係数=0 は値の純粋さを意味し、Gini係数を1から0へ近づけていくように、つまりある1水準がかたまるように分類していきます。分かりやすい例では、所得格差の大きい国は不平等なのでジニ係数は1に近いですが、高所得者の国と低所得者の国という２つの国に分けてしまえば、それぞれの国の中で見ると格差は小さくなり平等になるということになります。決定木でもこのように分岐していきます。なお、目的変数が量的変数の場合は、ノード内分散を分岐の指標に用いることがあります。

　CHAIDは、CARTが2分岐だったのに対し、一度に複数の分岐ができます。説明変数は基本的には質的変数である必要がありますが、量的変数もカテゴリ化すれば使用することができ、分析ツールではこれを自動的に処理する機能もあります。多分岐の構造をもつため、各変数が複数のカテゴリを持っていたり、カテゴリ（範囲）ごとのルールについて把握したい場合などに有用だといえます。分岐の指標にはカイ2乗統計量を使います。これは統計的検定の一種で、その分岐の差異に統計的な意味があるか判定する指標となります。なお、目的変数が量的変数の場合は、同じく統計的検定の手法であるF検定を用いることがあります。

　C5.0は、比較的最近の手法となり、CHAIDと同じく一度に複数の分岐ができます。なお目的変数は質的変数に限定されます。CHAIDのように多分岐の構造をとるため、各変数が複数のカテゴリを持っていたり、カテゴリ（範囲）ごとのルールについて把握したい場合などに有用だといえます。ただ、カテゴリ数の多い説明変数を好んで選択する傾向があり、モデルは複雑となる傾向があります。分岐の指標はエントロピーと呼ばれる、「事象の不確かさ」を示す指標を使います。エントロピーとは、何が起こるか予測できないとき最大で、発生確率の偏りが大きいほど小さくなります。決定木においては、エントロピーが低いほどノードの純度は高くなるので、この値が低くなるように分岐がされます。

　決定木はこうした特徴の異なるアルゴリズムによってアウトプットも異なります。そのため、どの手法を使えばよいのかという問いが多く発生します。その回答としては、どれが正解ということではなく、どれも正解であり、その選択に迷うときはそれぞれ実行してそれぞれの結果を確認し、設定したビジネス課題や適用業務との合致性を考慮して使用しやすい分析結果を選択するということで良いと思います。

要因把握の決定木と識別予測の決定木

　決定木は先述の通り、目的変数の特徴が色濃く現れるように、つまりその特徴にデータが偏るように説明変数を使ってデータを分割し、その分岐ルールをツリー構造で生成する機械学習の手法になります。アウトプットがツリー構造で可視化されるため、視覚的に目的変数と関係が強い要因を把握したり、その特徴が最も現れる条件ルールを把握することができます。一方、決定木はその条件ルールから目的変数の状態を予測する予測モデルとしても利用することができ、近年の人工知能ブームではその予測精度の追求で盛んにアルゴリズム開発の研究が行われています。
　決定木の予測精度を向上させる特にメジャーな方法として、バギングとブースティングがあります。バギングはランダムフォレストとも呼ばれることがありますが、すべてのデータで１つの決定木を生成するのではなく、データや説明変数の一部を抜き出して決定木を生成し、これを学習に使用するデータや説明変数を何度も入れ替えて多数の決定木を生成し、最後に得られたすべての決定木の結果を統合することで、１回の学習に依存しないで全体の予測精度を向上させるというものです。ブースティングはすべてのデータあるいは一部のデータでまず決定木を生成し、その予測結果で間違って予測されたデータの重みを重くして決定木を更新することで、その間違ったデータをうまく予測できるようにしていきます。この調整を繰り返して複数の決定木を生成し、最後にやはりそれらの結果を組み合わせることで予測精度を向上させるというものです。厳密な技術的説明は割愛しますが、このように複数の決定木を生成してそれを組み合わせることで予測精度を向上させるといったアルゴリズムの開発がされています。
　確かにこうした取り組みによって決定木の予測精度は向上していきますが、一方でシンプルさが失われていきます。複数の決定木を組み合わせることで、どの説明変数のどの閾値でデータが分割され、どのような要因・条件が目的変数に影響を与えているのかツリー構造で可視化できなくなってしまいます。これはベイジアンネットワークの解説のなかで記載しました「識別問題のディープラーニングと現象理解のベイジアンネットワーク」に通じるところがあり、どちらの手法がよいということではなく、それぞれの特徴を理解したうえで使い分けることが求められます。つまりデータの中の要因関係を理解することよりも予測精度の高さを追及する場合はバギングやブースティングを適用することはとても有効ですし、業務担当者が施策を検討するヒントを得るために、ある特定の効果を発揮する要因や条件を可視化してそのデータに潜む特徴や要因関係を理解したい場合は、予測精度は劣るかもしれませんがシンプルに一つの決定木をアウトプットするのが良いかと思います。

決定木とベイジアンネットワーク

　決定木では、説明変数の分岐条件の下において目的変数の分布を計算していきますが、実は左右対称のツリー構造を持つ決定木と子ノードが一つのベイジアンネットワークは等価となります。例えば下図のように目的変数Yに対して説明変数がX1とX2の2つがあり、どの変数も0と1の2水準を持つ変数であるとしたとき、X1で分岐がされたそれぞれのノードに対してどちらもX2で分岐したときの決定木は、X1とX2の全組み合わせに対してYの確率分布を計算するターミナルノードができあがります。これはX1とX2を親ノード、Yを子ノードとしたベイジアンネットワークと等価になり、この場合のベイジアンネットワークの確率モデルP(Y|X1,X2)はX1とX2の全組み合わせに対してYの確率分布を計算したモデルとなります。

※本解説記事の内容を引用または転載される場合は、その旨を明記いただくようにお願いいたします。