differential PLSA

differential PLSAの概要

differential PLSAとは、テキストデータの分析において、より個性的なトピックを抽出する技術です（特許登録済：特許第7221527号）。differential PLSAはPLSAを応用して開発したトピック抽出の技術ですが、通常のPLSAでは出現頻度の多い要素で構成される典型的なトピックが抽出されがちであるのに対し、differential PLSAでは頻度に依存しない個性的なトピックを抽出し、データ全体では埋もれがちな特徴を発見します。

differential PLSAの開発背景

　ビジネスにおけるデータ活用の場面では、特に新たな気づきとなるインサイトの獲得が期待されますが、実際にデータ分析から得られる結果は、経験的によく知っているものも多く、目新しさがないと評価されてしまうことがあります。実際に、データ分析の実行結果に対して、ビジネスの実務担当者からこのようなコメントが届くことがあります。たとえば、「この結果は経験的によく知っているのですが…」「わざわざ分析しなくても分かっていましたが…」「これまで見えてこなかった発見はないですか？」「ビジネスはもっとインサイトですよ！」などです。要するに、データ分析の結果に目新しさがなく、期待外れと評価されることがあります。

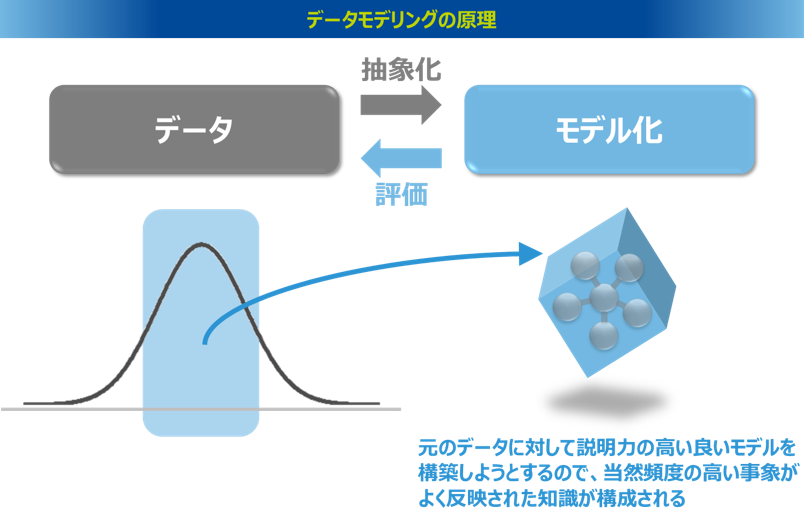
　しかし、これはデータ分析においてはとても自然なことです。そもそも、データ分析において「モデル化する」ということは、データに潜む傾向やルールを抽象化するということなので、元のデータに対して説明力の高いモデルを構築しようとすると、当然頻度の多い事象がよく反映されます。結果として経験的によく知っていることが優先的に表現されるということになります。経験的に分かっていることでも、その仮説をきちんとデータで示せたり、定性的な仮説を定量的な知識として獲得できることには十分価値があるはずですが、ビジネスの現場ではそれだけでは満足されないという現実があります。

　この問題はテキストデータからPLSAでトピックを抽出する分析にも該当するもので、PLSAではテキストデータ全体を表現するような典型的なトピックが抽出される傾向があります。次元圧縮法であるPLSAは、元の高次元のデータに対して、再現性の高い低次元のトピックに変換する手法であるため、元のデータに対して表現力の高いトピックが抽出されることになります。PLSAのインプットとなる共起行列は頻度を値とするデータですが、元のデータに対して表現力の高いトピックを抽出するには、当然頻度の高い要素を中心に代表的なトピックが形成される傾向があります。結果として高い頻度の要素で構成され、経験的によく知っているような、典型的とも感じられるトピックが抽出されるわけです。しかし、これはデータ全体の特徴を把握する上では有用な分析で、一つひとつのトピックはよく知っている典型的なものであっても、そうしたトピックに類型化することは人間では困難な処理のはずです。実際に結果に対して目新しさがないと感じる人は、結果を見たからそう感じているだけで、結果を見ないで自分の経験や感覚に基づいて、代表的なトピックを網羅的に列挙することはほぼできないはずです。

　当社では、典型的であってもデータ全体を表現するトピックを抽出することで、全体像を把握する分析の重要性を前提とするものの、より個性的なトピックも抽出できる手法としてdifferential PLSAを開発しました。

データに潜む特徴を抽象化するデータモデリングの原理

differential PLSAの技術的解説

通常のPLSA

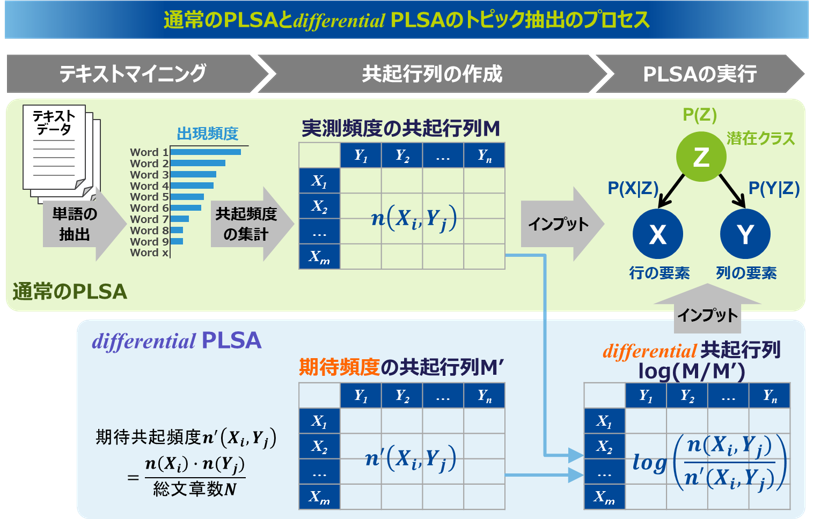
　differential PLSAはPLSAを応用したトピック抽出手法です。PLSAによるトピック抽出のプロセスをおさらいすると、まずテキストデータにテキストマイニングを実行して単語を抽出し、その単語群の共起頻度を集計した共起行列を作成します。そしてこの共起行列をインプットとしてPLSAを適用することで、関係性の強い行の要素と列の要素で構成されたトピックを抽出します。

differential PLSAの考え方

　通常のPLSAでインプットとする共起行列は、各要素の実際の共起頻度を集計したものですが、differential PLSAでは、これに加えて、各要素の全体の頻度割合から期待頻度を集計した共起行列を作成します。そしてこの２つの共起行列の各共起ペアにおいて、期待頻度に対する実測頻度の比率の対数を取った共起行列を作成し、これをインプットにPLSAを適用してトピックを抽出します。

　より具体的に解説すると、通常のPLSAでは、行要素Xと列要素Yが共起する実測頻度n(X,Y)を値として持つ共起行列Mを作成しますが、differential PLSAではこれに加えて、行要素Xと列要素Yが共起する期待頻度n’(X,Y )を値として持つ共起行列M’を作成します。期待頻度とは、行要素Xと列要素Yの総頻度（出現文章数）と、全体における出現割合に基づいて計算した理論値となります。具体的には、Xの総頻度（出現文章数）をn(X)、Yの総頻度（出現文章数）をn(Y)、総文章数をNとすると、行要素Xと列要素Yが共起する期待頻度とは、Xの総頻度n(X)に対して、Yの出現割合n(Y)/Nをかけた値となります。あるいは、列要素Yの総頻度n(Y)に対して、行要素Xの出現割合n(X)/Nをかけた値でも同じです。この実測頻度と期待頻度の2つの共起行列の考え方は、カイ二乗検定をするときに作成する観測度数と期待度数の2つのクロス集計表に近いイメージとなります。

　さらにdifferential PLSAでは、共起行列の各共起ペアにおいて、期待頻度に対する実測頻度の比率の対数を値として持つ共起行列（differential共起行列）を構築し、これにPLSAを適用します。期待頻度に対する実測頻度の比率に対数を取る理由は、極端に高くなる値を制限するためです。特に期待頻度は1未満となるケースも多く、比率のみでは値が高くなりすぎるものもあります。この状態では共起行列全体の値の分布は大きくばらつき、極端な値の開きが生まれてしまいます。この状態のままPLSAを適用すれば、この極端に大きな値に引っ張られる結果となるため、必要以上にデフォルメされた歪んだトピックとなることが懸念されます。そこでこの比率の値の「対数」を取ることで値の分布をならし、この問題を緩和します。なお、対数の計算において値が負数となるものは0に置換します。

通常のPLSAとdifferential PLSAのトピック抽出のプロセスの違い

differential PLSAの効果

　実測頻度の共起行列に適用する通常のPLSAでは、その解を求める最適化計算において（尤度最大化の計算過程において）、どうしても頻度が高い要素に高い確率が割り当てられ、結果として抽出されるトピックは典型的なものになる傾向があり、目新しさに欠けてしまいます。一方、differential PLSAの共起行列では、実測頻度を期待頻度で除した値の対数を取った共起行列をインプットとすることで、実測頻度が高い共起ペアでも、元々全体の頻度が高い要素が含まれるときには期待頻度も高い値となるため、実測頻度を期待頻度で除すことで値の大きさが制限されます。逆に、実測頻度が低い共起ペアでも、期待頻度がそれよりも十分小さければ比率の値は大きくなり、これにPLSAを適用した解では、こうした要素にも高い確率が割り当てられる可能性があります。つまり、通常のPLSAでは、頻度が低い要素には高い確率が割り当てられにくい傾向がありますが、differential PLSAでは、頻度が低くても共起関係が強い要素には高い確率が割り当てられる可能性があります。これによって、より個性的なトピックを抽出でき、データ全体では埋もれがちな特徴を発見することが期待できます。

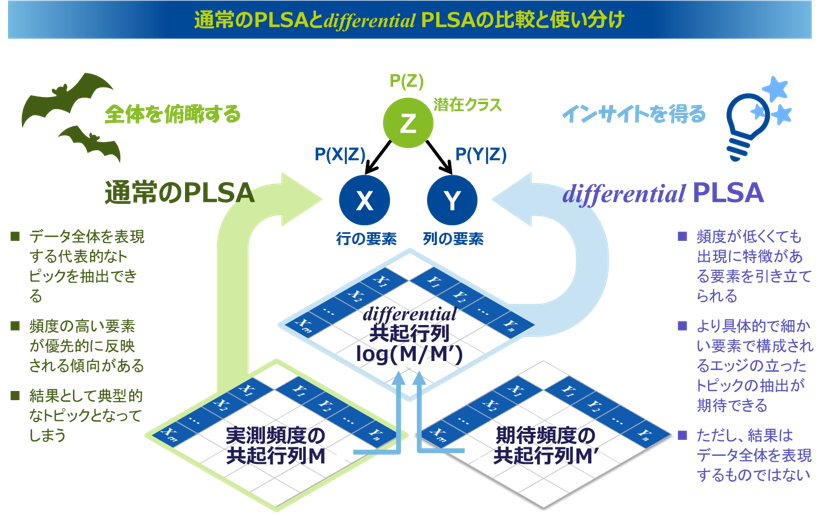
通常のPLSAとdifferential PLSAの使い分け

　differential PLSAは、より細かく具体的な要素で構成されるエッジの立ったトピックの抽出が期待できるので、特に新たな気づきとなるインサイトを獲得したい場面では効果的です。しかし、differential PLSAはインプットの共起行列を加工してしまっているので、結果は元のデータ全体を表現するものではなくなっていることに注意が必要です。データ分析の取り組みでは、木を見て森を見ずとならないように、まずは全体像を把握することが第一であり、全体像の現状を把握した上で個別性のある特徴を探ることが重要となります。データ全体を表現するようなトピックを把握し、全体像を俯瞰するなら、通常のPLSAを適用することが合理的です。そのため、differential PLSAは、あらかじめ通常のPLSAによって全体像を把握した上で適用することが有効だと考えています。

通常のPLSAとdifferential PLSAの比較と使い分け