自然言語処理コラム　～トピックモデル編～

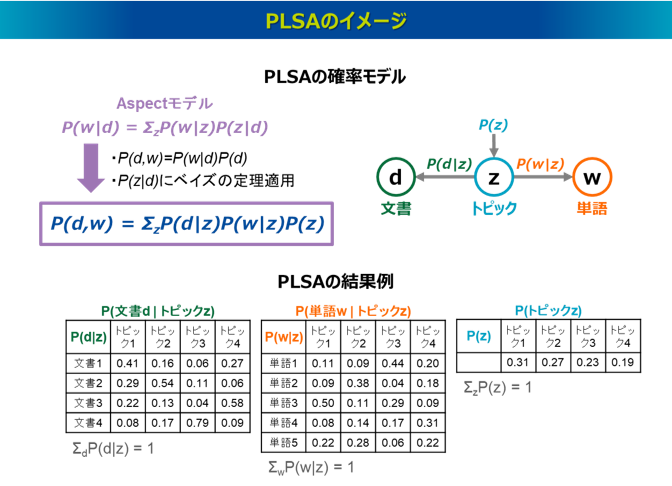
トピックモデル

　Bag-of-Wordsによる「文書×単語」の行列データをインプットに、教師なし学習で文書に潜むトピックをアウトプットする、「トピックモデル」と呼ばれる技術の各種手法について解説します。テキストマイニングでは、形態素解析で抽出された単語を単位に可視化や統計解析を実行し、文書全体の傾向を把握しようとしますが、トピックモデルでは、そうした単語群をいくつかのトピックに集約します。つまり、単語単位ではなく集約されたトピックを単位に文書全体の傾向を把握できる手法となります。

　大規模なテキストデータの場合、テキストマイニングでは膨大な単語が抽出されるため、その単語群をベースにした可視化はとても複雑になり、解釈性が薄れてしまいます。解釈性を向上させるために、Bag-of-Wordsのデータに対してクラスター分析で文書をグルーピングすることもあります、なかなか良い結果が得られにくいことが多いです。その理由として、Bag-of-Wordsは列となる単語の数が膨大でかなり高次元なデータとなるため、距離に基づいた通常のクラスター分析を実行してしまうと、データ間の距離がどれも非常に離れ、妥当な結果が得られにくくなる次元の呪いという問題が生じてしまうためです。これに対してトピックモデルでは、距離に基づかないでこの高次元データの次元数を削減し、膨大な単語群をトピックに集約することができます。これにより人間が文書をシンプルかつ効率的に理解するのに役立ちます。

　トピックモデルは主に2000年前後に開発が盛んとなった技術ですが、ここではその代表的な手法として「LSA」「NMF」「PLSA」「LDA」を取り上げて解説します。 

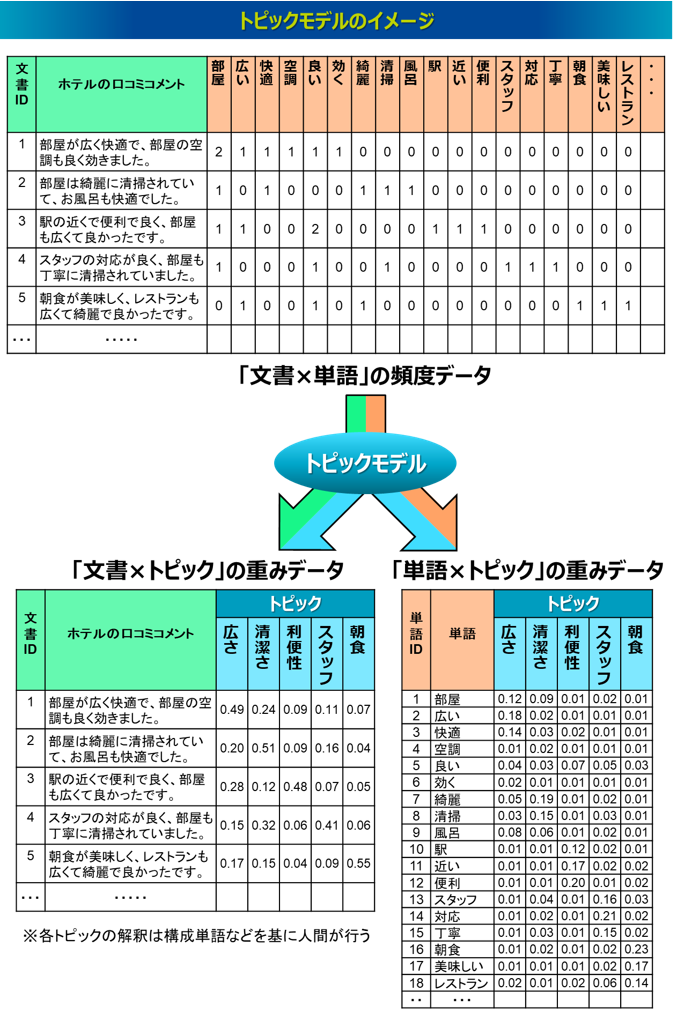
LSA

　LSA（Latent Semantic Analysis、潜在意味解析）は、Bag-of-Wordsによる「文書×単語」の行列をSVD（Singular Value Decomposition, 特異値分解）によって次元削減することでトピックを抽出する手法です。1990年に発表された手法ですが²⁾、その基礎となる考え方の研究はそれ以前から存在しています。情報検索の分野ではLSI（Latent Semantic Indexing）とも呼ばれています。

　LSAの具体的な処理は、「文書×単語」行列を①「文書×トピック」（左特異ベクトル）、②「トピック×トピック」（特異値）、③「トピック×単語」（右特異ベクトル）の3つの行列に分解することです。特異値「トピック×トピック」は対角行列で、その対角成分には特異値が大きい順に配列されます。左特異ベクトルの「文書×トピック」と右特異ベクトルの「トピック×単語」は、トピックを示すベクトル（左特異ベクトルでは各列、右特異ベクトルでは各行）が直交しており、各トピックの軸は数学的に互いに独立しています。SVDによる数学的な処理は、元の行列を最もよく近似する行列に分解すること、つまり元の行列と分解後の行列の誤差を最小化する最適化問題を解くことです。特に、SVDはこの最適解の存在が数学的に保証されているという点で強力で、計算過程のシンプルさから計算効率も高いメリットもあります。

　SVDに類似する手法にPCA（Principal Component Analysis, 主成分分析）があります。PCAはSVDを用いた分析手法と捉えることができます、両者の関係について簡単に説明します。PCAは元のデータセットの分散を最大化させる方向（主成分）を見つけ出し、最も情報量の多い特徴を抽出することを目指しています。その主成分の方向に元のデータを射影することで、元のデータの重要な情報を保持しながら次元を削減します。SVDは分散を最大化させるという目的で用いられるものではないですが、PCAを効率的に実行できる手法として用いられるため、PCAは特定の条件下におけるSVDの応用の一例と見ることができます。つまり、SVDはPCAよりも一般的な手法といえますが、実用面でいえば両者は同様の手法のように扱われることがあります。

　SVDは大きな値に引っ張られてトピックが抽出される傾向があるため、LSAを実行する際には、Bag-of-WordsにTF-IDFなどで重み付けした行列を用いることが多いです。またLSAの課題として、分解する行列の要素に負の値を許容しているため、結果の解釈が難しくなることや、結果が学習データに完全に依存するため、過学習を起こしやすく、新しい文書のトピックは推定できないことなどが挙げられます。

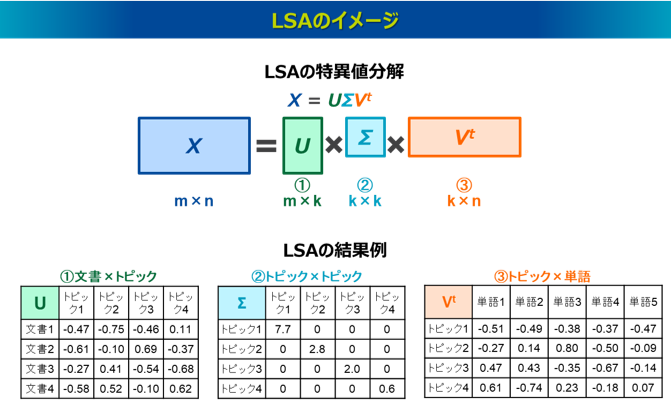
NMF

　NMF（Non-negative Matrix Factorization、非負行列因子分解）は、Bag-of-Wordsの「文書×単語」の行列を、2つの非負の行列「文書×トピック」と「トピック×単語」に分解することでトピックを抽出する手法で、1999年に発表されました³⁾。

　計算アルゴリズムは、元の行列と分解後の行列の積との誤差を最小化することを目的関数に、初期値を与えた反復計算により最適解を得ます。誤差の定義の仕方は、平方ユークリッド距離やKLダイバージェンスなどが使われます。反復計算は乗法更新式（Multiplicative update rule）が代表的で、これは得られる行列が必ず非負であるという制約条件化で適用される勾配降下法となります。LSAと比較して、分解後の行列の要素がすべて非負であるため、結果の解釈がしやすいメリットがあります。

　LSAと異なり、分解された「文書×トピック」と「トピック×単語」の行列は、各トピックのベクトル間で直交しておらず、各トピックは数学的に互いに独立していません。これにより、トピック間に意味的な重複が生じる可能性があります。また、LSAと同様に、NMFでも結果が学習データに完全に依存するため、過学習を起こしやすく、新しい文書のトピックは推定できないという課題があります。

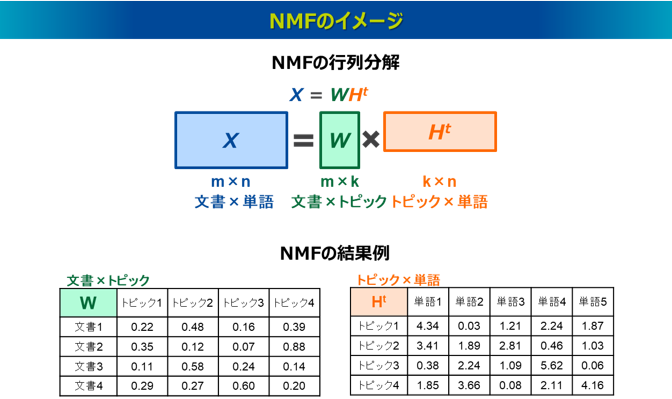
PLSA

　PLSA（Probabilistic Latent Semantic Analysis、確率的潜在意味解析）は、確率モデルを導入してトピックを抽出する手法です。特異値分解によってトピックを抽出するLSAの処理を確率的な枠組みによって発展させたもので、1999年に発表されました⁴⁾。情報検索の分野ではPLSI（Probabilistic Latent Semantic Indexing）と呼ばれることもあります。

　PLSAでは、Bag-of-Wordsの「文書×単語」の行列を確率的に分解することでトピックを抽出します。PLSAのモデルは文書dにおける単語wの出現確率P(w|d) を、潜在的なトピックzを介してモデル化したAspectモデルを起点としています（Aspectとは文書内に潜むトピックを指します）。Aspectモデルを式展開することで、文書dと単語wの同時確率P(d,w)を、3つの確率分布①P(d|z)、②P(w|z)、③P(z)に分解して表現します。この3つの確率分布をBag-of-Wordsの「文書×単語」行列データに基づき推定します。具体的には、P(d,w)の対数尤度関数を最大化するEMアルゴリズムを実行し、初期値を与えた反復計算により最適解を得ます。なお、PLSAはNMFとは異なる手法であり、NMFは確率的な仮定を置いたモデルではないですが、KLダイバージェンスを用いたNMFとPLSAが、同じ目的関数を最適化していると解釈できることが示されています⁵⁾。

　PLSAのメリットとして、LSAでは「文書×単語」の行列に対して事前にTF-IDFなどで重みづけする必要がありましたが、PLSAでは確率的な処理によりそうした重みづけをせずに実行することができます。また、PLSAは推定されるP(d|z)とP(w|z)によって、文書と単語のトピックに対する関連度が所属確率として出力されるため、結果が解釈しやすいメリットがあります。なお、各トピックは互いに独立しているという数学的な仮定を置いています。

　PLSAのデメリットとしては、入力する「文書×単語」のデータセットが大規模になると計算コストが高くなることが挙げられます。また、PLSAもLSAやNMFと同様に、結果が観測データに完全に依存するため、過学習を起こしやすく、新しい文書のトピックは推定できないという課題がありますが、一方で、観測データに対する再現度は高く、その観測データ固有の特徴をそのまま反映できるモデルと捉えることもできます。

LDA

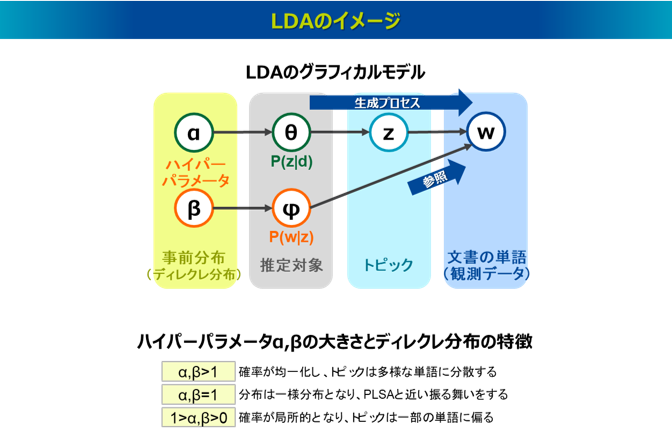
　LDA（Latent Dirichlet Allocation、潜在ディリクレ配分法）は、PLSAをベイズ的に拡張させた手法で、ディレクレ分布を事前分布に導入しており、2003年に発表されました⁶⁾。トピックモデルの中では最もよく使われる手法といえます。

　LDAは確率的な生成モデルともいわれ、文書d内の各単語wが特定のトピックzから生成されたと仮定します。このトピックzの分布は文書dごとに異なり、その確率分布P(z|d)はθで表されます。一方、特定のトピックzが各単語wを生成する確率分布P(w|z)はφで表し、そのトピックzの下で単語wを生成するプロセスではφが参照されます。つまり、LDAではθ→z→wという生成プロセスが仮定され、その中でz→wというアローの確率過程はφ→wというアローによる確率分布φが参照されます。なお、θとφはそれぞれハイパーパラメータαとβを持つディレクレ分布に従います。LDAの推定対象はθ=P(z|d)とφ=P(w|z)ですが、これらの生成過程を逆にたどるアルゴリズムにより、単語w（観測データ）からθとφを推定します。具体的には、各文書d中の各単語w（観測データ）に対して、まずその単語wがどのトピックzから生成されたと考えられるか、θとφの暫定値（初期値）から推定し（zの推定）、そしてその結果を基にして、各文書dがどのトピックzをどれだけ含むか推定し（θの推定）、各トピックzがどの単語wを生成する可能性が高いか推定します（φの推定）。これを繰り返すことでθとφを逐次的に更新していきます。推定アルゴリズムは、ギブスサンプリングや変分ベイズ法などが適用され、反復的に計算されます。

　PLSAはパラメータが固定的で、観測データのみから直接推定するため、結果が完全に観測データに依存していますが、LDAはパラメータが事前分布に従って変動する確率分布とし、観測データと事前分布から推定します。事前分布を導入することで、確率的なスムージング効果があり、過学習を抑制できます。また、LDAは新しい文書についても推定ができ、新しい文書に対応するθを未知とし、新しい文書に含まれる単語w（観測データ）と学習済みのφとαからθを推定します。

　一方、LDAはハイパーパラメータαとβによって結果が変動しやすく、この値の設定の仕方、推定の仕方が難しいという課題があります。ハイパーパラメータα,βの大きさとディレクレ分布の特徴は、α,β>1では、値が大きいほど確率が均一化し、どの文書も同じようなトピックの分布を持つようになり、トピックは多様な単語に分散して関連づけられる傾向があります。α,β=1では分布は一様分布となり、様々なトピックにランダムに確率が割り当てられます。これは事前分布を仮定していないPLSAと近い振る舞いをします。1>α,β>0では、値が小さいほど確率が局所的になり、文書は特定のトピックに確率が集中し、トピックは一部の単語に偏って関連づけられる傾向があります。また、LDAは新しい文書の推定ができる高い汎化性能を持つ一方で、トピックの結果が一般的で抽象度が高くなることがあります。

　なお、PLSAとLDAはどちらも文書dと単語wの関係をモデル化している手法ですが、文書dと単語wの関係の扱い方の違いには注意が必要です。PLSAの推定対象はP(d|z)とP(w|z)ですが、「文書d×単語w」の行列データに対して文書dと単語wの役割には対称性があり、行と列を入れ替えても推定結果に影響はありません。一方、LDAの推定対象はP(z|d)とP(w|z)ですが、文書dと単語wの役割は対称的ではなく、それぞれの役割は明確に区別されたモデルとなっています。そのため、行と列を入れ替えて適用すれば異なる結果となります。

参考文献

2) S. Deerwester, S.T. Dumais, G.W. Furnas, T.K. Landauer, and R. Harshman: "Indexing by Latent Semantic Analysis”, Journal of the American Society for Information Science, Vol.41, No.6, pp.391-407 (1990)

3) D. D. Lee and H. S. Seung: "Learning the parts of objects by non-negative matrix factorization," Nature, vol.401, pp.788–791 (1999

4) T. Hofmann: "Probabilistic Latent Semantic Analysis," Proc. of the 15th Conference on Uncertainty in Artificial Intelligence, pp.289–296  (1999)

5) C. Ding, T. Li, and W. Peng; "Nonnegative Matrix Factorization and Probabilistic Latent Semantic Indexing: Equivalence, Chi-square Statistic, and a Hybrid Method," Proc. of the 21st National Conference on Artificial Intelligence, pp.342-347 (2006)

6) D. M. Blei, A. Y. Ng, and M. I. Jordan: "Latent Dirichlet Allocation," Journal of Machine Learning Research, Vol.3, pp.993–1022  (2003)

続いて「深層学習モデル編」はこちら